题目链接
Luogu 3195
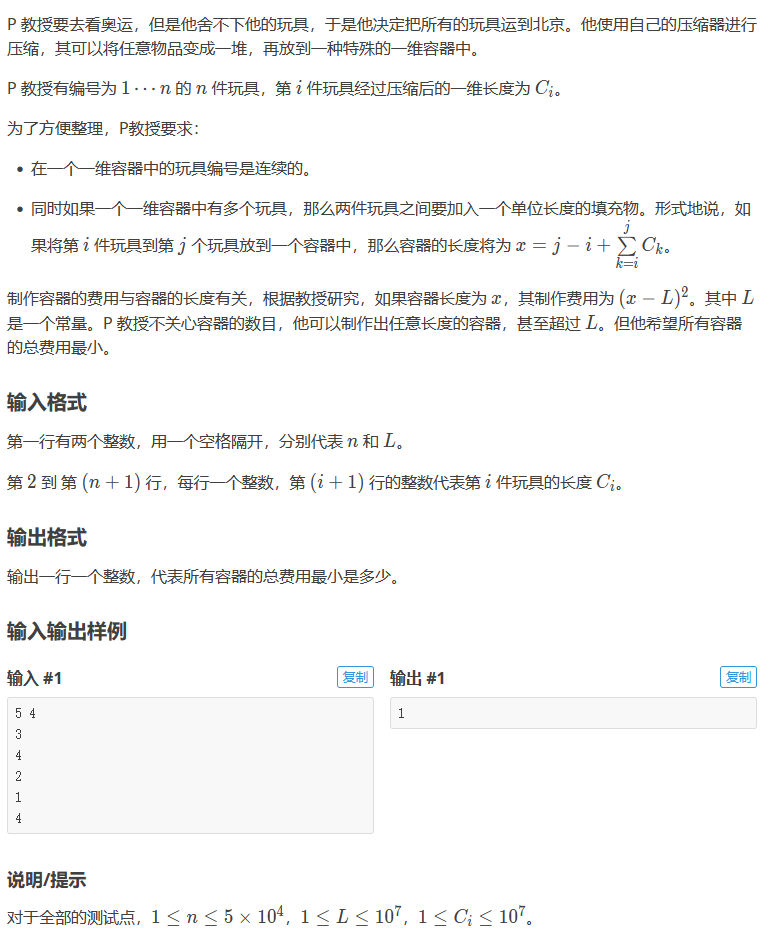
题目描述
题解
暴力
设$dp[i]$为处理前$i$个玩具的最小花费,$a[i]$为前$i$个玩具长度的前缀和。
易得转移方程为$dp[i]=min \lbrace dp[j]+(i−j−1+a[i]−a[j]−l)^2 \rbrace (0 \leq i < j \leq n)$
此方法时间复杂度为$O(n^2)$,只能水到20分。
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int N=50005;
long long n,l,dp[N],a[N];
int main()
{
scanf("%lld%lld",&n,&l);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]),a[i]+=a[i-1];
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
for(int i=1;i<=n;i++)
for(int j=0;j<i;j++)
dp[i]=min(dp[i],dp[j]+(i-j-1+a[i]-a[j]-l)*(i-j-1+a[i]-a[j]-l));
printf("%lld",dp[n]);
}
|
单调性
观察该题数据范围和状态只有一维的转移方程,我们可以尝试通过斜率优化将时间复杂度降到$O(n)$。
斜率优化中涉及单调队列的使用,自然要求方程满足决策单调性,一般可以通过决策表的方法进行验证,对于此题来说,数据容易生成,可以尝试一下。
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int N=50005;
long long n,l,dp[N],a[N],best[N];
int main()
{
scanf("%lld%lld",&n,&l);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]),a[i]+=a[i-1];
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
for(int i=1;i<=n;i++)
for(int j=0;j<i;j++)
dp[i]=min(dp[i],dp[j]+(i-j-1+a[i]-a[j]-l)*(i-j-1+a[i]-a[j]-l)),best[i]=j;
for(int i=1;i<=n;i++)printf("%d",best[i]);
printf("%lld",dp[n]);
}
|
易观察到$best[i]$单调不降,满足决策单调性。
证明见下:
对于$dp[i]$,当其由$dp[k]$转移而来优于$dp[j]$时,有
$$dp[k]+(i−k−1+a[i]−a[k]−l)^2 < dp[j]+(i−j−1+a[i]−a[j]−l)^2$$
$$dp[k]−dp[j] < (i−j−1+a[i]−a[j]−l)^2−(i−k−1+a[i]−a[k]−l)^2$$
对于该方程,可设
$$b[i]=a[i]+i$$
$$l=l+1$$
则有
$$dp[k]−dp[j]<(b[i]−b[j]−l)^2−(b[i]−b[k]−l)^2$$
化简得
$$((dp[k]+b[k]^2)−(dp[j]+b[j]^2))/(b[k]−b[j])<2b[i]−2l$$
此时的形式为点斜式方程:
$$(yk−yj)/(xk−xj) < ansi$$
已知$b[i]$为前缀和的形式,所以$b[i]$单调递增,可知斜率为单调递增。则适用决策单调性。
设
$$g[k,j]=(yk−yj)/(xk−xj)$$
则当且仅当$g[A1,A2] < b[i]−2l$时,由$A1$转移而来优于$A2$。
当$g[c,b] < g[b,a]$时,易证得$b$必不为最优决策。
当$g[c,b] < ansi$,此时$c$决策优于$b$,则$b$一定不为最优决策。
当$g[c,b]>=ansi$,此时$b$决策优于$c$,但又有$g[b,a]>g[c,b]>=ansi$,此时$b$决策不优于$a$决策。
综上所述,则可将所有满足$g[c,b] < g[b,a]$的决策$b$排除掉。此时函数满足上凸的性质,即有斜率递减。
具体方法
以下我们便可以进行斜率优化(严格建立在决策单调性的基础上):
1: 用单调队列维护点集信息。
2: 求解$dp[i]$,可以从队首开始扫描,当$g(head+1,head) < ansi$时,可知$head+1$优于$head$,故继续扫描,直到不满足条件,此时$bext[i]=head$,即使$dp[i]$最优的决策为队首。
3: 当加入点$i$,我们要维护队列的上凸性质,即从队尾开始扫描,判断$g(i,tail)$是否小于$g(tail,tail-1)$,如果满足,则可删除$tail$,并继续扫描,直到不满足该条件,则$i$在此处入队,队列仍满足上凸性质。
AC代码如下:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 50005;
long long n,l,a[N],b[N],dp[N],q[N];
double g(long long k,long long j)
{
return ((dp[k]+b[k]*b[k])-(dp[j]+b[j]*b[j]))/(b[k]-b[j]);
}
int main()
{
scanf("%lld%lld",&n,&l);
for(int i=1;i<=n;++i)scanf("%lld",a+i),a[i]+=a[i-1];
for(int i=1;i<=n;++i)b[i]=a[i]+i;
l++;
int head=1,tail=1;
q[1]=0;
for(int i=1;i<=n;++i)
{
while(head<tail&&g(q[head+1],q[head])<2*b[i]-2*l)head++;
int j=q[head];
dp[i]=dp[j]+(b[i]-b[j]-l)*(b[i]-b[j]-l);
while(head<tail&&g(i,q[tail])<g(q[tail],q[tail-1]))tail--;
q[++tail]=i;
}
printf("%lld",dp[n]);
}
|


