可持久化线段树总结

本文移植自个人的原博客（原文）

定义

主席树又称可持久化线段树，相对与普通的线段树，其解决的是各种不适用于结合律的区间问题，诸如区间第$K$大，区间种类个数等。

线段树的每个结点，保存的是这个区间含有的数字的性质的结合。

主席树的每个结点，保存的元素以元素大小为第一维位置，同时保证以区间为第二维位置，直接实现是$O(nlog^2n)$的时间空间复杂度，即每一个区间都要建一棵树，考虑每颗线段树的大小和形态是一样的，那么我们便可以利用主席树之间相互进行加减运算的性质，进行可持久化建树。

具体过程是按区间位置进行建树，每次插入新的数，只需要重新插入一条链，因为对于那些性质没有改变的前缀（如插入元素的位置是$3$，那么节点：$[1,2]$就没有必要改变），只需要重新调用皆可，否则利用原节点建一个新的节点（如插入元素的位置是$3$，那么节点：$[3,4]$的性质一定发生了改变，但又要保证原区间的该节点性质不变，那么便可以先将该节点粘过来，再在此基础上建一个新的节点，插入在当前根节点下），这样时间空间复杂度均降到了$O(nlogn)$（可持久化线段树按权值建树，其时间复杂度实际与权值范围有关（所以要离散化），本文全部以$n$代替）。

当然，这样实现也会导致整个数据结构实际上完全不是一棵树了，但是却仍满足每个节点最多有两个后继的限制，因此查询时只要调用$l−1,r$两个根节点即可。

相关题目

NEERC 2004 K小数

题目链接

COGS 1534

题目描述

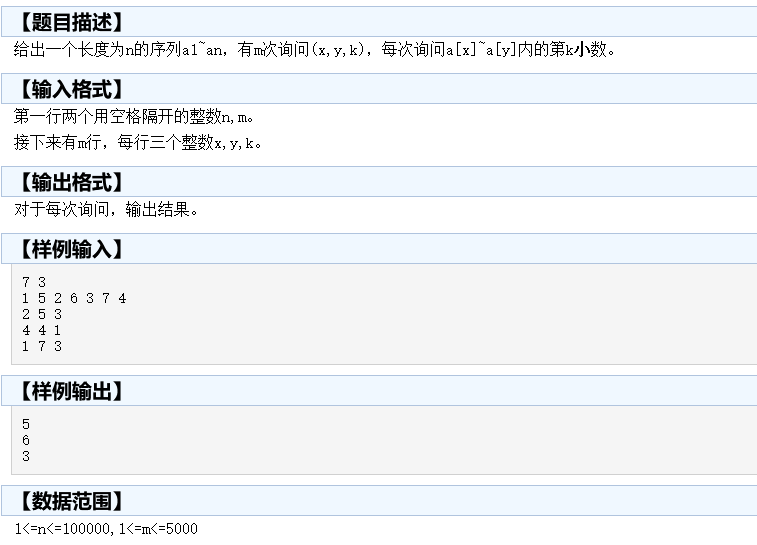
题解

实现与按权值维护的平衡树类似，直接递归查询即可。

#include<algorithm>
#include<cstdio>
using namespace std;
const int N = 1e5+1;
int n,m,totn,a[N],b[N];
struct nd{int ls,rs,sum;}t[N*20];
int tot,root[N];
void insert(int l,int r,int x,int &y,int v)
{
    y=++tot;
    t[y]=t[x];t[y].sum+=1;
    if(l==r)return;
    int mid=l+r>>1;
    if(v<=mid)     insert(l,mid,t[x].ls,t[y].ls,v);
    else         insert(mid+1,r,t[x].rs,t[y].rs,v);
}
int get(int l,int r,int x,int y,int k)
{
    if(l==r)return l;
    int mid=(l+r)>>1;
    int v=t[t[y].ls].sum-t[t[x].ls].sum;
    if(v>=k)     return get(l,mid,t[x].ls,t[y].ls,k);
    else         return get(mid+1,r,t[x].rs,t[y].rs,k-v);
}
int main()
{
//    freopen("kthnumber.in","r",stdin);
//    freopen("kthnumber.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]),b[i]=a[i];
    sort(b+1,b+n+1);
    totn=unique(b+1,b+n+1)-b-1;
    for(int i=1;i<=n;i++)
      insert(1,totn,root[i-1],root[i],lower_bound(b+1,b+totn+1,a[i])-b);
    for(int i=1,x,y,z;i<=m;i++)
      scanf("%d%d%d",&x,&y,&z),
      printf("%d\n",b[get(1,totn,root[x-1],root[y],z)]);
}

SDOI2009 HH的项链

题目链接

COGS 421

题目描述

题解

对于每一个元素，记录其在数列内下一个种类相同的元素的位置（以 $to$ 数组表示），那么问题就转化为了求区间内有多少个元素的 $to$ 值大于查询的右区间位置，将 $to$ 数组插入到主席树中，直接建树求解即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 5e4+1;
struct nd{int rs,ls,sum;}t[N*25];
int a[N],tot,b[N],totn,n,m,root[N],vis[N],to[N];
void insert(int l,int r,int x,int &y,int k)
{
    y=++tot;
    t[y]=t[x];
    t[y].sum++;
    if(l==r)return;
    int mid=l+r>>1;
    if(k<=mid)    insert(l,mid,t[x].ls,t[y].ls,k);
    else        insert(mid+1,r,t[x].rs,t[y].rs,k);
}

int get(int l,int r,int x,int y,int v)
{
    if(r<v)return 0;
    if(l>=v)return t[y].sum-t[x].sum;
    int mid=l+r>>1;
    return get(l,mid,t[x].ls,t[y].ls,v)+get(mid+1,r,t[x].rs,t[y].rs,v);
}

int main()
{
    freopen("diff.in","r",stdin);
    freopen("diff.out","w",stdout);
    scanf("%d",&n);
    for(int i=1,x;i<=n;++i)
    {
        scanf("%d",&x);
        if(vis[x])to[vis[x]]=i;
        vis[x]=i;
    }
    for(int i=1;i<=n;++i)if(!to[i])to[i]=n+1;
    for(int i=1;i<=n;++i)
    insert(1,n+1,root[i-1],root[i],to[i]);
    scanf("%d",&m);
    for(int i=1,l,r;i<=m;++i)
    {
        scanf("%d%d",&l,&r);
        printf("%d\n",get(1,n+1,root[l-1],root[r],r+1));
    }
}

动态排名系统

题目链接

COGS 257

题目描述

题解

本题为裸的带修改区间第$K$大，如果直接在例$1$的基础上修改，则会导致超时，因为每次修改都要修改$nlogn$个节点，即最坏情况下每一个根都要修改$log$个没有指向前面节点的节点。那么可以考虑，主席树维护的实际上是数列的前缀的性质，可以利用树状数组优化，即将原先的对于每一个新元素的前缀建树，改为对于树状数组中的前缀建树，那么修改时只要修改$log^2n$个节点即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define lowbit(x) x&(-x)
using namespace std;
const int N = 8e6+1;
struct nd{int ls,rs,sum;}t[N];
int T,n,m,A[N],B[N],C[N],b[N],a[N],X[N],Y[N],root[N],totx,toty,totn,tot;
char s[3];
void insert(int l,int r,int x,int &y,int k,int v)
{
    y=++tot;
    t[y]=t[x];
    t[y].sum+=v;
    if(l==r)return;
    int mid=l+r>>1;
    if(k<=mid)    insert(l,mid,t[x].ls,t[y].ls,k,v);
    else        insert(mid+1,r,t[x].rs,t[y].rs,k,v);
    return;
}


void add(int x,int v)
{
    int k=lower_bound(b+1,b+totn+1,a[x])-b;
    for(int i=x;i<=n;i+=lowbit(i))
    insert(1,totn,root[i],root[i],k,v);
}
int query(int l,int r,int k)
{
    int sum=0,mid=l+r>>1;
    if(l==r)return l;
    for(int i=1;i<=totx;++i)sum-=t[t[X[i]].ls].sum;
    for(int i=1;i<=toty;++i)sum+=t[t[Y[i]].ls].sum;
    if(k<=sum)
    {
        for(int i=1;i<=totx;++i)X[i]=t[X[i]].ls;
        for(int i=1;i<=toty;++i)Y[i]=t[Y[i]].ls;
        return query(l,mid,k);
    }
    else
    {
        for(int i=1;i<=totx;++i)X[i]=t[X[i]].rs;
        for(int i=1;i<=toty;++i)Y[i]=t[Y[i]].rs;
        return query(mid+1,r,k-sum);
    }
}



int main()
{
    freopen("dynrank.in","r",stdin);
    freopen("dynrank.out","w",stdout);
    scanf("%d",&T);
    while(T--)
    {
        memset(root,0,sizeof(root));
        memset(C,0,sizeof(C));
        totn=tot=0;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;++i)
        scanf("%d",a+i),b[++totn]=a[i];
        for(int i=1;i<=m;++i)
        {
            scanf("%s%d%d",s,A+i,B+i);
            if(s[0]=='Q')    scanf("%d",C+i);
            else            b[++totn]=B[i];
        }
        sort(b+1,b+totn+1);
        totn=unique(b+1,b+totn+1)-b-1;
        for(int i=1;i<=n;++i)add(i,1);
        for(int i=1;i<=m;++i)
        if(C[i])
        {
            totx=toty=0;
            for(int j=A[i]-1;j;j-=lowbit(j))X[++totx]=root[j];
            for(int j=B[i];j;j-=lowbit(j))    Y[++toty]=root[j];
            printf("%d\n",b[query(1,totn,C[i])]);
        }
        else
        {
            add(A[i],-1);
            a[A[i]]=B[i];
            add(A[i],1);
        }
    }
}

国家集训队2011 数颜色

题目链接

COGS 1901

题目描述

题解

同样是记录 $to$ 数组，对于修改操作，可以暴力求出修改后该位置 $to$ 的变化，考虑一下可能造成的在该元素前的元素的 $to$ 指针的变化即可（注意同样要修改主席树），详见代码。（对于$to$数组的查询和修改可以用平衡树优化）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define lowbit(x) x&(-x)
using namespace std;
typedef int ll;
const ll N = 1e4+1;
struct nd{ll ls,rs,sum;}t[N*600];
ll n,m,a[N],b[N],X[55],Y[55],A[N],B[N],C[N],to[N],vis[1000001];
ll root[N],totn,tot,totx,toty;
char s[3];

void insert(ll l,ll r,ll x,ll &y,ll k,ll v)
{
    if(!y){y=++tot;t[y]=t[x];}
    t[y].sum+=v;
    if(l==r)return;
    ll mid=l+r>>1;
    if(k<=mid)    insert(l,mid,t[x].ls,t[y].ls,k,v);
    else        insert(mid+1,r,t[x].rs,t[y].rs,k,v);
    return;
}

void add(ll x,ll v)
{
    for(ll i=x;i<=n+1;i+=lowbit(i))
    insert(1,n+1,root[i],root[i],to[x],v);
}

ll get(ll l,ll r,ll v)
{
    if(r<v)return 0;
    if(l>=v)
    {
        ll sum=0;
        for(ll i=1;i<=totx;++i)sum-=t[X[i]].sum;
        for(ll i=1;i<=toty;++i)sum+=t[Y[i]].sum;
        return sum;
    }
    ll X1[55],Y1[55];
    for(ll i=1;i<=totx;++i)X1[i]=X[i];
    for(ll i=1;i<=toty;++i)Y1[i]=Y[i];

    ll mid=l+r>>1;
    ll sum=0;
    for(ll i=1;i<=totx;++i)X[i]=t[X1[i]].ls;
    for(ll i=1;i<=toty;++i)Y[i]=t[Y1[i]].ls;
    sum+=get(l,mid,v);

    for(ll i=1;i<=totx;++i)X[i]=t[X1[i]].rs;
    for(ll i=1;i<=toty;++i)Y[i]=t[Y1[i]].rs;
    sum+=get(mid+1,r,v);
    return sum;
}
int main()
{

    freopen("nt2011_color.in","r",stdin);
    freopen("nt2011_color.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(ll i=1,x;i<=n;++i)
    {
        scanf("%d",&x);
        a[i]=x;
        if(vis[x])to[vis[x]]=i;
        vis[x]=i;
    }
    for(ll i=1;i<=n;++i)if(!to[i])to[i]=n+1;
    for(ll i=1;i<=m;++i)
    {
        scanf("%s%d%d",s,A+i,B+i);
        if(s[0]=='R');
        else C[i]=1;
    }
//    sort(b+1,b+totn+1);
    for(ll i=1;i<=n;++i)add(i,1);
    for(ll i=1;i<=m;++i)
    {
        totx=toty=0;
        if(C[i])
        {
            memset(X,0,sizeof(X));
            memset(Y,0,sizeof(Y));
            for(ll j=A[i]-1;j;j-=lowbit(j))    X[++totx]=root[j];
            for(ll j=B[i];j;j-=lowbit(j))    Y[++toty]=root[j];
            printf("%d\n",get(1,n+1,B[i]+1));
        }
        else
        {
            add(A[i],-1);
            a[A[i]]=B[i];
            to[A[i]]=n+1;
            for(ll t=A[i]+1;t<=n;++t)
            if(a[t]==B[i]){to[A[i]]=t;break;}
            add(A[i],1);
            for(int j=A[i]-1;j>=1;--j)
            {
                if(to[j]==A[i])
                {
                    add(j,-1);
                    to[j]=n+1;
                    for(int t=j+1;t<=n;++t)
                    if(a[t]==a[j]){to[j]=t;break;}
                    add(j,1);
                }
                if(a[j]==B[i]&&to[j]>A[i])
                {
                    add(j,-1);
                    to[j]=A[i];
                    add(j,1);
                }
            }
        }
    }
}

/*
6 6
1 1 1 2 2 2
Q 1 3
R 2 2
Q 1 3
R 3 2
Q 1 3
Q 1 2
*/