动态树总结

本文移植自个人的原博客（原文）

概念

动态树可以维护动态的森林，支持树的合并（LINK），拆分（CUT），动态LCA，换根，和所有树链剖分能支持的操作。动态树与树链剖分的区别在于树链剖分以线段树为基础，而动态树以SPLAY（按深度维护）为基础，这使得动态树相较前者可以支持动态的操作。

动态树中也有轻重链的概念，但其实现并不基于子树大小，而是在操作的过程中进行修改，使得每次需要操作的链处于同一SPLAY树中。需要特别说明的是，动态树对于子树的操作并不支持，但仍可以通过维护轻链的信息来完成简单点的操作。

核心操作

动态树的核心操作有：

ACCESS：将x到root的路径变为重链。（将x一步一步向上跳，每次将其变为父亲的重儿子）

MAKEROOT：将x变为root。（ACCESS(x)并将x旋转到该重链的根，然后对该平衡树进行翻转操作，使得x到root的深度顺序反转。）

SPLIT：将x与y加入同一颗SPLAY树中。（将x变为根节点，再ACCESS(y)）

LINK：树的合并。（将x变为所在树的根节点，并将其接到y上。注意son数组记录的是SPLAY中关系，而fa数组记录的是整棵树和SPLAY树的关系。所以此处不需要更新son数组）

例题

动态树

题目链接

COGS 2701

题目描述

题解

本题难点在于对于子树大小的查询，在常规的LCT中，只有重儿子的信息。此题可以通过维护轻儿子的信息来实现，本题中SIZE数组维护的是子树大小而不是SPLAY中的信息，VIR数组维护的是轻儿子的信息。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 2e5+1;
int son[N][2],mx[N],sum[N],w[N],size[N],rev[N],tag[N],fa[N],vir[N];
int n,m;

bool isnotrt(int x){return son[fa[x]][0]==x||son[fa[x]][1]==x;}

//void add(int x,int val)
//{
//    w[x]+=val;mx[x]+=val;
//    sum[x]+=size[x]*val;
//    tag[x]+=val;
//    return;
//}

void up(int x)
{
    int l=son[x][0],r=son[x][1];
    size[x]=size[l]+size[r]+vir[x]+1;
//    sum[x]=sum[l]+sum[r]+w[x];
//    mx[x]=max(max(mx[l],mx[r]),w[x]);
}

void down(int x)
{
    int &l=son[x][0],&r=son[x][1];
    if(rev[x])
    {
        rev[l]^=1;rev[r]^=1;
        swap(l,r);
        rev[x]=0;
    }
//    if(tag[x])
//    {
//        add(son[x][0],tag[x]);
//        add(son[x][1],tag[x]);
//        tag[x]=0; 
//    }
    return;
}

void rotate(int x)
{
    down(fa[x]);down(x);
    int y=fa[x],z=fa[y],t=(son[y][0]==x);
    if(isnotrt(y)) son[z][son[z][1]==y]=x;fa[x]=z;
    son[y][!t]=son[x][t];fa[son[y][!t]]=y;
    son[x][t]=y;fa[y]=x;
    up(y);up(x);
}

void splay(int x)
{
    down(x);
    while(isnotrt(x))
    {
        int y=fa[x],z=fa[y];
        if(isnotrt(y))
        {
            if(son[y][0]==x^son[z][0]==y)rotate(x);
            else    rotate(y);
        }
        rotate(x);
    }

}

void access(int x)
{
    for(int y=0;x;y=x,x=fa[x])
    {
        splay(x);
        vir[x]-=size[y];
        vir[x]+=size[son[x][1]];
        son[x][1]=y;
        up(x);
    }
}

void makert(int x){access(x);splay(x);rev[x]^=1;}

void split(int x,int y){makert(x);access(y);splay(x);}

void link(int x,int y){makert(y);fa[y]=x;vir[x]+=size[y];}

void cut(int x,int y){split(x,y);son[x][1]=fa[y]=0;}

int find(int x){access(x);splay(x);while(son[x][0])x=son[x][0];return x;}
int main()
{
    freopen("dynamic_tree.in","r",stdin);
    freopen("dynamic_tree.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=1,x;i<=n;i++)size[i]=1;
    for(int i=1,opt,x,y,z;i<=m;++i)
    {
        scanf("%d%d",&opt,&x);
        if(opt==1) makert(x);
        else if(opt==2)
        {
            access(x);
            printf("%d\n",vir[x]+1);
        }
        else if(opt==3) {scanf("%d",&y);int z=find(x);link(x,y);makert(z);}
    }
}
/*

6 11
3 2 3
3 4 5
3 2 4
3 6 2
2 1
2 5
3 1 2
2 4
1 3
2 1
2 4

*/

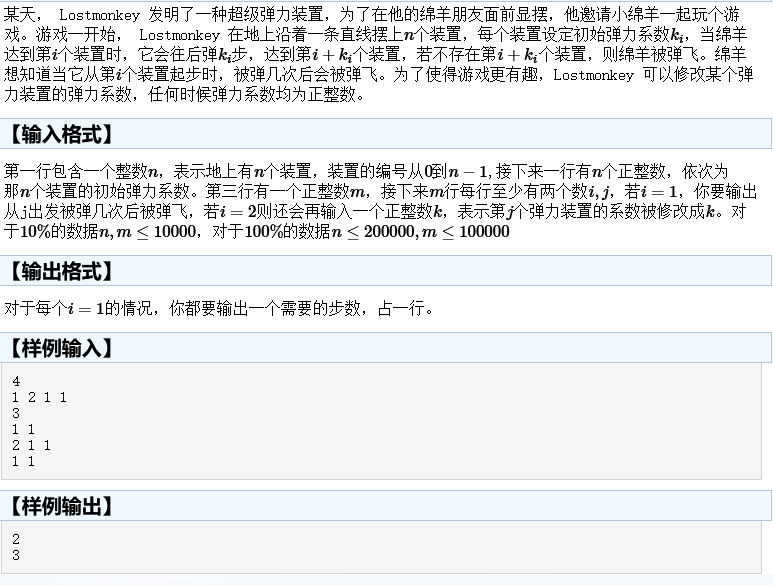
HNOI2010 弹飞绵羊

题目链接

COGS 1689

题目描述

题解

由于每个点的目标节点唯一，所以可以将其看为倒置的一棵树。设立一个哨兵节点$n+1$，每个会弹出去的位置都指向哨兵节点。

那么每次查询实际上就是求$x$到根节点的链的长度，可以将链加入同一颗SPLAY中，然后查询SPLAY大小即可。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 3e5+1;
int k[N],n,m,son[N][2],fa[N],size[N],sum[N],rev[N];

void up(int x){size[x]=size[son[x][0]]+size[son[x][1]]+1;}

void down(int x)
{
    if(rev[x])
    {
        rev[x]^=1;
        rev[son[x][0]]^=1;
        rev[son[x][1]]^=1;
        swap(son[x][0],son[x][1]);
    }
}

int isrt(int x){return son[fa[x]][0]!=x&&son[fa[x]][1]!=x;}

void rotate(int x)
{
    down(fa[x]);down(x);
    int y=fa[x],z=fa[y],t=son[y][0]==x;
    if(!isrt(y))son[z][son[z][1]==y]=x;fa[x]=z;
    son[y][!t]=son[x][t];fa[son[x][t]]=y;
    son[x][t]=y;fa[y]=x;
    up(y);up(x);
}

void splay(int x)
{
    down(x);
    while(!isrt(x))
    {
        int y=fa[x],z=fa[y];
        if(!isrt(y))
        {
            if(son[y][0]==x^son[z][0]==y)rotate(x);
            else    rotate(y);
        }
        rotate(x);
    }
}

void access(int x)
{
    for(int y=0;x;y=x,x=fa[x])
    {splay(x);son[x][1]=y;up(x);}
}

void makert(int x){access(x);splay(x);rev[x]^=1;}

void split(int x,int y){makert(x);access(y);splay(x);}

void link(int x,int y){makert(x);fa[x]=y;}

void cut(int x,int y){split(x,y);son[x][1]=fa[y]=0;}



int main()
{
    freopen("bzoj_2002.in","r",stdin);
    freopen("bzoj_2002.out","w",stdout);
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&k[i]);
        if(k[i]+i>=n+1)k[i]=n+1-i;
        link(i,i+k[i]);
        size[i]=1;
    }
    size[n+1]=1;
    scanf("%d",&m);
    for(int i=1;i<=m;++i)
    {
        int op,x,val;
        scanf("%d%d",&op,&x);
        x++;
        if(op==1)
        {
            makert(n+1);
            makert(x);
            printf("%d\n",size[x]-1);
        }
        else
        {
            scanf("%d",&val);
            cut(x,x+k[x]);
            k[x]=val;
            if(k[x]+x>=n+1)k[x]=n+1-x;
            link(x,x+k[x]);
        }
    }
}