本文移植自个人的原博客（原文）

题目链接

Product Transformation

题目描述

题目描述

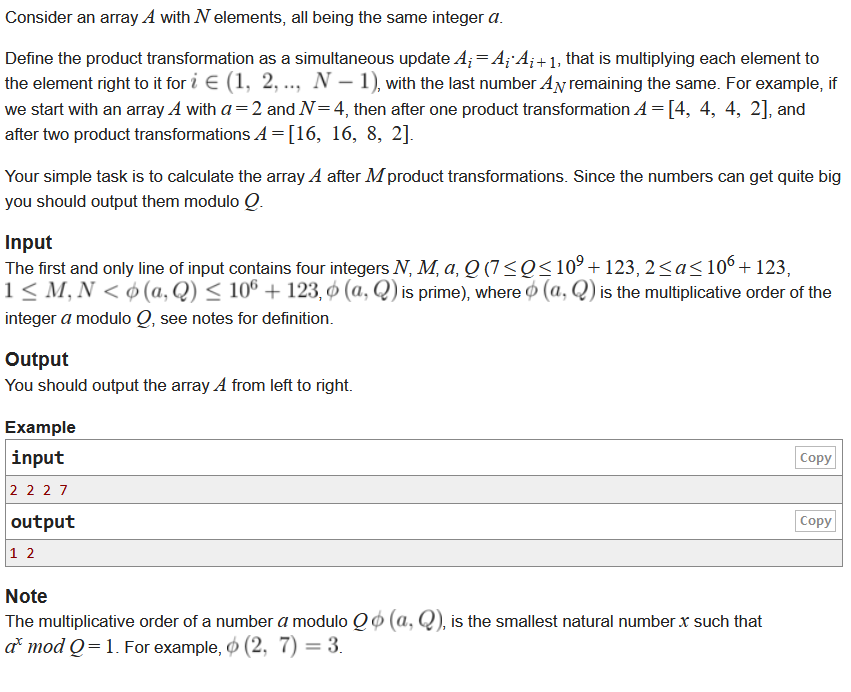
题解

已知数列中的底数全部相等，所以可以将操作看为指数相加，即

$$S_i=S_i+S_{i+1}$$

那么以$S_{i,j}$表示处理了几次，递推式如下：

$$S_{i,j}=S_{i−1,j}+S_{i,j+1}$$

初始化为$S_{0,j}=1$（即$a$的$1$次方）

将序列翻转，容易发现其递推式与组合数完全相同，只是初始化有些差异，组合数的初始化为$S_{0,0}=1$。考虑将两者进行转化。

容易发现，当$S_{0,j}=1(j<1)$时，两者完全相同，而当$S_{0,j}=1(j<2)$时，原式实际变为了杨辉三角形中代表的组合数与其右移一个单位后代表的组合数之和。一般性的，有
$S_{i,j}=\sum_{t=0}^{n-1}C_{i,j-t}$,即$S$为$C$的前缀和，那么只要计算出$C(m+1,i−1)$即可。

但是该题中$n,m$的范围均较大，所以必须用递推阶乘与阶乘逆元的方法求解，考虑题目中实际要对指数进行取模，且有满足$a^P=1(mod Q)$的最小$P$为质数，那么我们可以暴力求出这个$P$然后将指数对其取模。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6+1;

ll n,m,a,mod,rev[N],fac[N],ans[N],P;
ll qpow(ll a,int b,ll mod)
{
    ll ret=1;
    while(b)
    {
        if(b&1)ret=ret*a%mod;
        b>>=1;
        a=a*a%mod;
    }
    return ret;
}
void pre()
{
    fac[0]=1;
    for(int i=1;i<=m;++i)fac[i]=fac[i-1]*i%P;
    rev[m]=qpow(fac[m],P-2,P);
    for(int i=m-1;i>=0;--i)rev[i]=rev[i+1]*(i+1)%P;
}
ll C(ll n,ll m)
{
    return n<m?0:fac[n]*rev[m]%P*rev[n-m]%P;
}

int main()
{
//       2  2  2  7
    cin>>n>>m>>a>>mod;
    if(mod==1){for(int i=1;i<=n;++i)cout<<0<<" ";return 0;}
    ll now=1;
    for(int i=1;;++i)
    {
        now=now*a%mod;
        if(now==1){P=i;break;}

    }
    pre();
    for(int i=1;i<=n;++i)
    ans[i]=C(m,i-1);

    for(int i=1;i<=n;++i)(ans[i]+=ans[i-1])%=P;
    for(int i=1;i<=n;++i)ans[i]=qpow(a,ans[i],mod);
    for(int i=n;i>=1;--i)printf("%I64d ",ans[i]);
//static int c[101][101],f[101][101];
//    for(int i=0;i<=10;++i)
//    {
//        c[i][i]=1;
//        for(int t=1;t<i;++t)
//        c[i][t]=c[i-1][t]+c[i-1][t-1];
//    }
//    for(int i=1;i<=10;++i)f[1][i]=f[i][1]=1;
//    for(int i=2;i<=10;++i)
//    for(int t=2;t<=10;++t)
//    f[i][t]=f[i-1][t]+f[i-1][t-1];
//    
//    for(int i=1;i<=10;++i)
//    {
//        for(int t=1;t<=i;++t)
//        cout<<c[i][t]<<" ";
//        cout<<endl;
//    }
//    
//    for(int i=1;i<=10;++i)
//    {
//        for(int t=1;t<=i;++t)
//        cout<<f[i][t]<<" ";
//        cout<<endl;
//    }
//    
//    for(int i=1;i<=10;++i)
//    {
//        for(int t=1;t<=i;++t)
//        cout<<f[i][t]-c[i][t]-c[i][t-1]-c[i][t-2]<<" ";
//        cout<<endl;
//    }
}