线性代数的几何意义
基于3Blue1Brown科普内容的总结,关于线性代数的本质。
3Blue1Brown原视频链接
张成与基
向量集合的张成是所有能表示的点所构成的线性空间。
基即最小的向量集合,使得该集合的张成等于当前线性空间。
线性变换
线性变换是指满足可加性,数乘性的离散函数,有输入,有输出。通俗来说,线性变换的几何意义是原点不变且直线在变换后仍为直线,更直观的表示是原点不变且网格线变换前后保持平行且等距离。
矩阵与矩阵乘法
矩阵的几何意义是线性变换,矩阵乘法的几何意义是线性变换的叠加。
行列式
方阵的行列式的几何定义是有向的放缩倍率。
非方阵
非方阵也是高维到低维的线性变换。
点积
点积的式子可以用对偶性来证明,看成对于一个向量的非方阵线性变换,使得其位于另一个向量的直线上。
叉积
二维叉积是有向面积,就是将其看作二维线性变换后的放缩倍率,即行列式。
三维叉积的面积即将两个向量和另一个单位向量(看作可变向量,但将其认为是单位向量)看作三维线性变换后得到的放缩倍率,即行列式。但最终得到的行列式实际上是个与两个向量垂直的向量,且长度才为叉积值。此处可以用对偶性来证明,将该行列式等同于求得向量与可变向量的点积,显然无论该可变向量如何变化都是成立的,可变向量在所求向量上的投影=可变向量在六面体的高,所求向量长度=底面积叉积,所以叉积的本质就是这个求得向量。
特征向量与特征值
特征向量是线性变换中张成空间不变的向量。
特征值是特征向量的变化率。($A*v=\lambda*v$,$A$是线性变换矩阵,$\lambda$是特征值,$v$是特征向量)
相似对角化
$A^{-1}*M*A$实际上是在非标准基下进行标准视角下的变换。(比如说旋转$90$度,标准基下乘上$M$即可,但是非标准基下要乘上$A^{-1}*M*A$,$A$是用来转化成标准基的线性变换矩阵)
如果可以选$n$个特征向量张成整个空间的话,那么可以将这$n$个向量看作新的基底,此时线性变换在该基底下一定是对角阵,即有$A^{-1}*M*A=D$。($D$是对角阵)(基向量都是特征向量的话,线性变换一定是对角阵)
方阵快速幂:



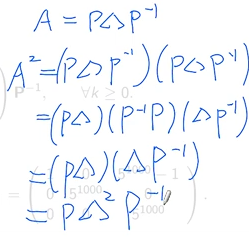
向量的抽象
满足八大公理的结构都能被看作向量,存在线性变换,也有之前所推导的性质。例如函数也可以看作一种有无穷维度的向量,同样有基底($1,x^1,x^2,x^3,…$)。线性变换即线性算子(如求导等,可以用无穷阶的方阵表示),点积即内积,特征向量即特征函数等等。


