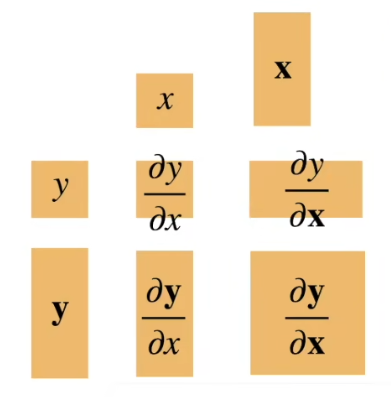动手学深度学习笔记 6-损失函数
Github主页课程主页教材
L2 Loss 优势在于离最优点越近,梯度越小,起到微调的效果,且使得损失函数收敛。劣势在于当离最优点过远时,梯度可能会过于大,导致在最优点的两侧反复横跳,收敛过慢。
L2 Loss 优势在于离最优点过远时,梯度不会特别大。劣势在于当离最优点过近时,无法进一步逼近,无法收敛。
可以看到 L1 Loss 和 L2 Loss 的优势是互补的,因此有 Huber’s Robust Loss 在离最优点近时采用 L2,在离最优点远时采用 L1,结合了两者的优势。 ...
动手学深度学习笔记 5-多层感知机
Github主页课程主页教材
关于多层感知机的知识,还需要结合更深入的学习进一步理解。
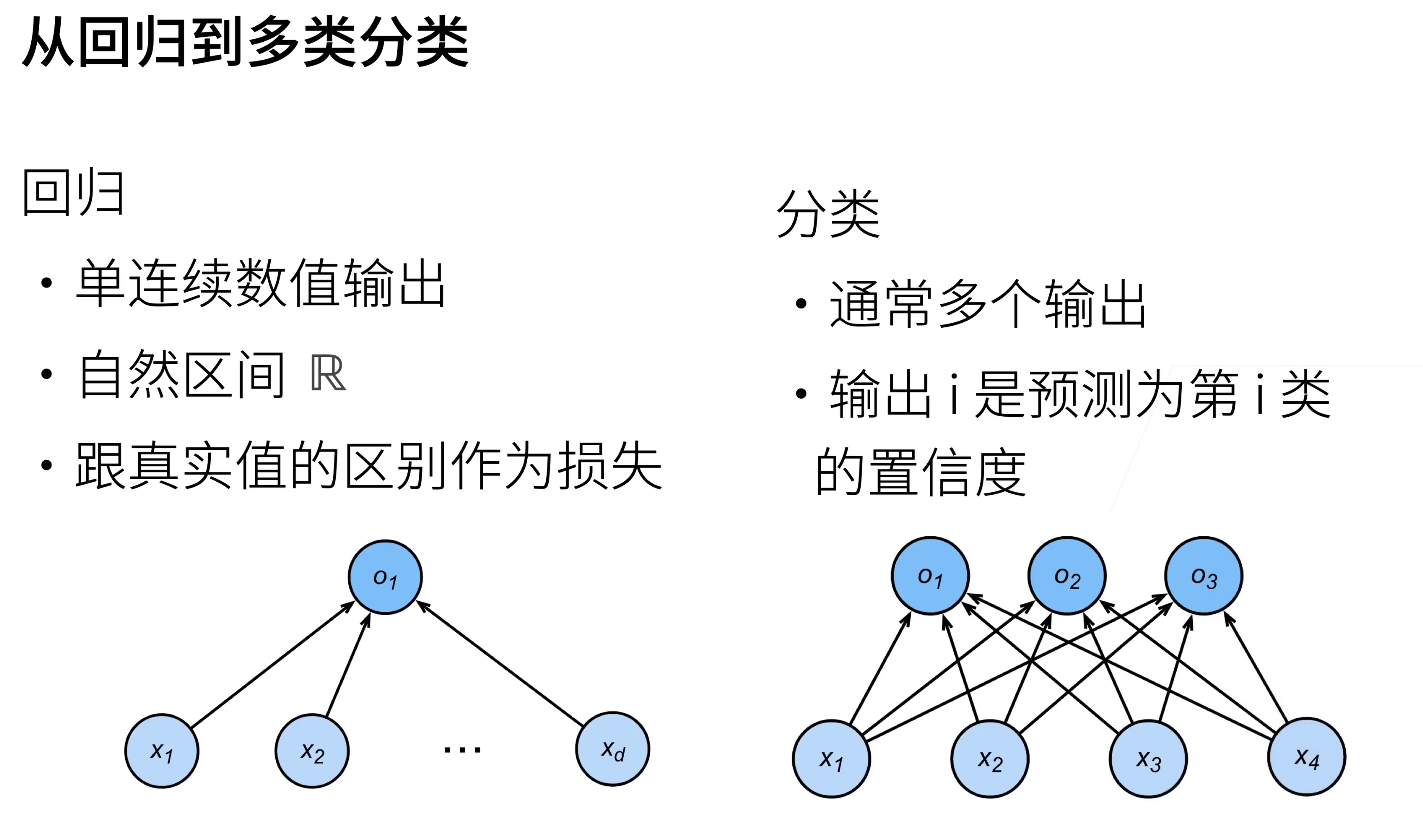
动手学深度学习笔记 4-softmax回归
Github主页课程主页教材
softmax 可以看作支持多分类的逻辑回归,关于逻辑回归的推导可看logistic回归原理与实现,关于 softmax 的推导,可看softmax回归原理与实现
softmax 的数学基础来自统计学习方法,收到热力统计学启发而得。
关于 softmax 的数学内容,在 d2l 教材中有着更详细的说明。
动手学深度学习笔记 3-梯度下降
Github主页课程主页教材
WSL 2 下配置深度学习环境
Windows 10 + WSL 2 + Ubuntu 22.04 + CUDA 11.6 + CUDAToolkit 11.6 + Miniconda 3 + cuDNN 8.4.1 + VSCode + Xming
WSL 2 常用命令
WSL 2 是一种在 Windows 中内置的 Linux 子系统。
动手学深度学习笔记 2-自动求导
Github主页课程主页教材
反向传播相比正向传播的优势
自带剪枝。
对所有变量求偏导可以在一次传播过程中完成。
反向传播相比正向传播的劣势
空间复杂度为$O(n)$,每个没有被剪枝的节点都需要同时存储在内存中。
动手学深度学习笔记 1-矩阵求导
Github主页课程主页教材
关于矩阵求导的详细技巧,可见矩阵求导术一文。
本源勾股数
题解本源勾股数$(x,y,z)$满足:
$x^2+y^2=z^2$
$gcd(x,y,z)=1$
$x,y,z \in Z^+$
本源勾股数$(x,y,z)$可用以下公式推导:
$x=m^2-n^2$
$y=2mn$
$z=m^2+n^2$
其中$(m,n)$满足:
$m>n$
$gcd(m,n)=1$
$ m+n \equiv 1 (mod \ 2) $
$m,n \in Z^+$
其中寻找互质数对$(m,n)$需要用到$Stern-Brocot \ Tr ...
Markdown与Mathjax的冲突
关于Markdown与Mathjax的冲突以及解决方案。